APÉNDICE 12.1 - PRUEBAS ESTADÍSTICAS
PRUEBA t DE STUDENT - COMPARACIÓN DE MEDIAS DE MUESTRAS
Para determinar si la velocidad media de un conjunto de mediciones de velocidad es significativamente diferente de otra (es decir, entre un estudio anterior y otro posterior), es apropiado utilizar la prueba t de Student de dos colas, partiendo de la hipótesis razonable de que las varianzas de los dos conjuntos de mediciones se extraen de la misma población. La hipótesis nula es, por tanto, que no hay diferencia en las medias (es decir, que el programa no ha afectado a la velocidad de los conductores). En primer lugar, es necesario determinar la desviación estándar de la diferencia en las medias. A continuación, calculamos las ecuaciones siguientes:

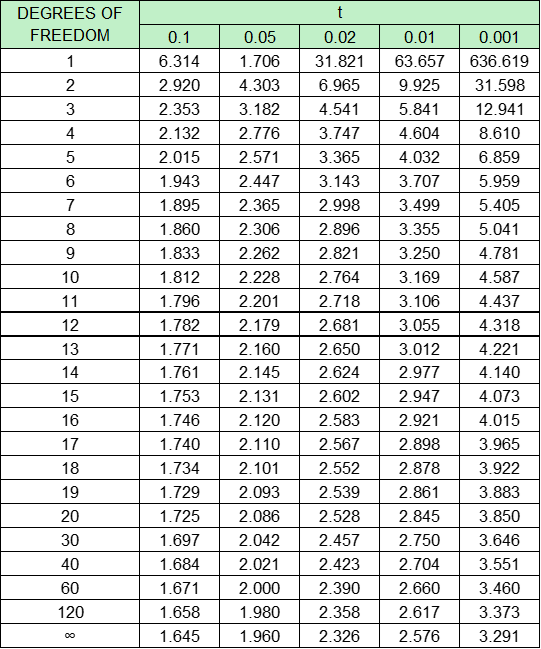
Una vez calculado el valor de t, debemos consultar una tabla de valores t de Student (Tabla 12.A1) con (na + nb – 2) grados de libertad (ʋ). Si el valor calculado de t supera el del nivel del 5 % (la columna t = 0,05), podemos estar seguros al 95 % de que la velocidad media real ha cambiado.
Ejemplo
Supongamos que los siguientes resultados se obtuvieron de estudios de velocidad puntual:

De la ecuación [ECUACIÓN. 12.1]:

Como el valor t calculado (9,69) es mayor que 1,96 (gran número de grados de libertad), podemos decir que la diferencia en las velocidades medias (una reducción de 4 km/h) es significativa al nivel del 5 %.
Esta prueba se puede realizar con la CALCULADORA: PRUEBA DE DISTRIBUCIÓN
TABLA 12.A1: TABLA DE DISTRIBUCIÓN T
PRUEBA DE KOLMOGOROV-SMIRNOV
La prueba "bilateral" determina si dos muestras independientes se han extraído de la misma población (o de poblaciones con la misma distribución). En algunos casos, dos conjuntos de datos pueden tener la misma media, pero una dispersión diferente, lo que puede ser la causa de problemas de seguridad. Si las dos muestras se han extraído de la misma población (la hipótesis nula), entonces cabe esperar que las distribuciones acumulativas de ambas muestras estén bastante próximas entre sí, es decir, que solo muestren una desviación aleatoria de las distribuciones de la población. Si las distribuciones acumulativas de las dos muestras se alejan demasiado en algún punto, esto sugiere que proceden de poblaciones diferentes. Por consiguiente, una desviación suficientemente grande entre las distribuciones acumulativas de las dos muestras es una prueba para rechazar la hipótesis nula.
Sea SNa(x) la función de distribución acumulada observada de la primera muestra de velocidad: es decir, SNa(x) = K/Na donde K es el número de vehículos iguales o inferiores a x km/h y Na es el número total de vehículos de la muestra. Sea SNb(x) la función de distribución acumulada de la segunda muestra. Ahora la prueba bilateral de Kolmogorov-Smirnov se centra en la desviación máxima, D.
Para muestras grandes (N > 40), las tablas de Kolmogorov-Smirnov muestran que el valor de D debe ser igual o superior al siguiente valor para rechazar la hipótesis nula al nivel del 5 %, es decir, que no son de la misma población:
La prueba "unilateral" determina si las dos muestras se han extraído de la misma población o si los valores de una muestra son estocásticamente mayores que los valores de la población de la que se extrajo la otra muestra. La desviación máxima se calcula de nuevo utilizando [ECUACIÓN 12.2] y la significación del valor observado de D puede calcularse por referencia a la distribución chi-cuadrado.
Se ha demostrado que, para muestras grandes, la siguiente estadística presenta una distribución muestral que se aproxima a la distribución chi-cuadrado con dos grados de libertad. La tabla chi-cuadrado se muestra en la Tabla 12.A2.
CALCULADORA: PRUEBA DE DISTRIBUCIÓN
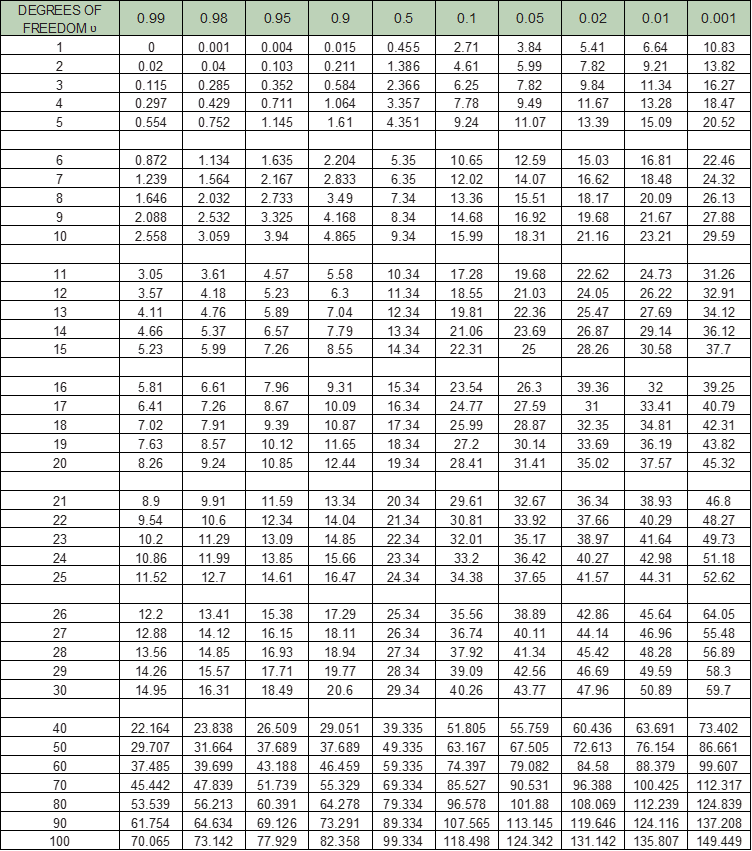
TABLA 12.A2: TABLA DE X2
PRUEBA k
La prueba k puede utilizarse para mostrar cómo han cambiado los números de accidentes en un sitio en comparación con los datos de control.
Para un sitio especifico o un grupo de sitios tratados de manera similar, tenemos:
donde:
a = Accidentes en el sitio “antes”
b = Accidentes en el sitio “después”
c = Accidentes en el sitio de control “antes”
d = Accidentes en el sitio de control “después”
Si k < 1 entonces ha habido una disminución del número de accidentes en relación con el control.
Si k = 1 entonces no ha habido ningún cambio en relación con el control.
Si k > 1 entonces ha habido un aumento en relación con el control.
Si alguna de las frecuencias es cero, entonces se debe añadir ½ a cada una, es decir:
El cambio porcentual en el lugar viene dado por:
Ejemplo La Tabla 12.A3 muestra los totales anuales de accidentes con heridos en una intersección en T en una zona semiurbana que originalmente tenía señales de stop en la carretera secundaria, pero donde se instaló una rotonda hace tres años. Los datos de control utilizados son los accidentes en todas las demás intersecciones prioritarias del distrito durante exactamente los mismos períodos de 3 años antes y 3 años después. TABLE 12.A3: FRECUENCIAS DE ACCIDENTES CON LESIONES EN EL SITIO TRATADO Y EN LOS CONTROLES
Utilizando la notación y la ecuación anteriores: Por lo tanto, como k < 1, ha habido una disminución en los números de accidentes en relación con los controles de: (k-1) x 100% = 68% Esta prueba se puede realizar con la CALCULADORA: PRUEBAS ANTES – DESPUÉS (SITIO INDIVIDUAL). |
LA PRUEBA DE CHI - CUADRADO
Esta prueba se puede utilizar para determinar si el cambio en los accidentes fue producido por el tratamiento u ocurrió por casualidad. Entonces, la prueba determina así si el cambio es estadísticamente significativo. Se basa en una tabla de contingencia que muestra tanto los valores observados de un conjunto de datos (O) como los valores esperados correspondientes (E). La estadística de chi-cuadrado viene dada por:
Donde:
Oij = valor observado en la columna j, fila i de la tabla
Eij = valor esperado en la columna j, fila i de la tabla
m = número de columnas
n = número de filas
A continuación, se utiliza una tabla de chi-cuadrado para buscar este valor, que muestra la probabilidad de que el valor “esperado” y los valores “observados” se extraigan de la misma población. También se requiere el número de grados de libertad, que viene dado por:
Grados de libertad (ʋ) = (n – 1) (m – 1)
Para una evaluación de accidentes en un sitio, en la que los accidentes se comparan en períodos similares antes y después de la intervención, junto con un conjunto de sitios de control para los mismos períodos, tenemos una tabla de contingencia de 2 por 2 (2 columnas y 2 filas con grados de libertad = 1). Para que la prueba sea válida, el valor de cualquier celda de la tabla no debe ser inferior a 5.
Utilizando la notación de la Tabla 12.A3, el valor de la chi-cuadrado se puede calcular mediante la siguiente ecuación:

Este valor se compara entonces con los valores de la chi-cuadrado de la Tabla 12.A2 con grados de libertad, ʋ = 1, y si es mayor que un valor determinado, se dice que es estadísticamente significativo al menos en ese nivel porcentual.
Ejemplo Utilizando los datos del ejemplo anterior y la [ECUACIÓN 12.9], obtenemos: 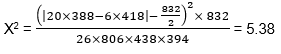 Ahora, si nos fijamos en la tabla de distribución de chi-cuadrado (Tabla 12.A2) y en la primera línea (un grado de libertad, ʋ =1), el valor de chi-cuadrado de 5,38 se encuentra entre 3,84 y 5,41. Esto corresponde a un valor de nivel de significación (en la línea de encabezado de columna) de entre 0,05 y 0,02. Esto significa que solo hay un 5 % de probabilidad (o 1 de cada 20 posibilidades) de que el cambio en los accidentes se deba a una fluctuación aleatoria. Otra forma de decirlo es que hay un 97,9 % de confianza de que se ha producido un cambio real en los accidentes en la intersección. El nivel del 5 % o superior se acepta ampliamente como indicativo de que la medida correctiva ha funcionado con certeza, aunque el nivel del 10 % puede considerarse indicativo de un efecto. |
GRUPO DE SITIOS CON EL MISMO TRATAMIENTO
Para un número de sitios, N, que han recibido el mismo tratamiento, determinar el efecto global requiere un cálculo bastante más complejo, es decir, resolviendo la siguiente ecuación para k en todos los sitios, es decir, i = 1 a N. Los demás símbolos son los mismos que en las ecuaciones anteriores.

Para realizar las pruebas, el logaritmo natural de una variable suele tener una distribución más simétrica (susceptible de tratamientos estadísticos estándar) y el error estándar de loge k puede aproximarse a lo siguiente:

La siguiente proporción debe calcularse utilizando el loge de la variable k calculada anteriormente y su error estándar a partir de la expresión anterior:

Y si este valor está fuera del rango ±1,96 (t de Student), entonces el cambio es estadísticamente significativo (al nivel del 95%).
Ahora, para comprobar si los cambios en lossitios tratados están produciendo de hecho el mismo efecto en las frecuencias de accidentes, necesitamos calcular el siguiente valor de chi-cuadrado.
Si es significativo con N-1 grados de libertad (consulte la fila número 1) en la tabla de chi-cuadrado, donde N es el número de sitios tratados), entonces los cambios en los sitios no están produciendo el mismo efecto. Sin embargo, si no es significativo, es probable que los cambios estén produciendo el mismo efecto.
CALCULADORA: PRUEBA ANTES – DESPUÉS (GRUPO DE SITIOS)
REGRESIÓN A LA CORRECCIÓN DE LA MEDIA
Para corregir el efecto de regresión a la media, se debe estimar el nivel de seguridad (o la frecuencia media de accidentes a largo plazo). Varios estadísticos han propuesto diferentes formas de hacerlo. Por ejemplo, Hauer (1992) recomendó utilizar el método Método empírico de Bayes para estimar el nivel de seguridad y luego utilizar este valor en estudios de seguridad (en vez de los datos brutos). En cambio, Abbess et al. (1981) describieron previamente un enfoque más simple para un solo sitio, en el que los datos se ajustaron para corregir sesgos utilizando suposiciones sobre la distribución de accidentes durante un período de varios años.
Los datos de accidentes deben recopilarse para zonas que sean similares al sitio tratado durante el mismo período de tiempo. Utilizando este conjunto de datos completo, se calculan el número medio de accidentes, a, y la varianza de los accidentes, m var (a). El efecto de regresión a la media, R (en %), viene dado por la siguiente ecuación:

donde:
A = número de accidentes en el sitio
n = número de años

At y nt son las estimaciones de los parámetros de la distribución estadística que muestran las frecuencias reales subyacentes de accidentes, es decir, la distribución de probabilidad de la frecuencia de accidentes antes de que se disponga de datos. Entonces, la hipótesis principal es que el sitio de estudio con un historial de accidentes concreto se comportará de la misma manera que el conjunto de todos los sitios similares con el mismo historial de accidentes.
Ejemplo Consideremos una intersección que ha tenido un promedio de 15 accidentes por año en los últimos 5 años. El espacio se amplió, se instalaron nuevas señales grandes de intersección, islas separadoras y señales de ALTO, después de lo cual el sitio ha tenido un promedio de 10 accidentes por año durante un período similar. Para corregir el efecto de regresión a la media, necesitamos seleccionar intersecciones similares no controladas con flujos de tráfico similares. Si todos estos han producido una media, a, de 12,6 accidentes por año con una varianza, var (a), de 2,91, los valores de entrada son: a = 12,6 accidentes/año var(a) = 2,91 (accidentes/año)2 A = 75 accidentes/5 años n = 5 años At = 12.62 / (2.91 – 12.6) = –16.38 nt = 12.6 / (2.91 – 12.6) = –1.3 Por lo tanto, el efecto de regresión: En otras palabras, durante el período posterior esperaríamos que, si no se hiciera nada en el sitio, los accidentes se reducirían en un 5,6 %, o a 14,16 accidentes por año. De manera que, es la cifra de 14,16 accidentes por año la que debe compararse con los 10 accidentes por año que realmente se produjeron para determinar si la reducción de la frecuencia de accidentes debido a las mejoras es estadísticamente significativa. |






