ANNEXE 12.1 – TESTS STATISTIQUES
TEST DE STUDENT – COMPARAISON DE MOYENNES D’ÉCHANTILLONS
Pour savoir si la vitesse moyenne d’un échantillon de mesures de vitesses est significativement différente de celle d’un autre échantillon (par exemple dans le cadre d’une étude avant-après), il est approprié d’effectuer un test de Student bilatéral, en posant comme hypothèse que les variances des 2 échantillons de données sont extraits d’une même population. L’hypothèse nulle est donc qu’il n’y a pas de différence entre les moyennes (c’est-à-dire la vitesse des conducteurs n’a pas été influencée par l’intervention). Il faut au préalable calculer l’écart type de la différence entre ces moyennes. On calcule ensuite les équations suivantes :

Il faut alors comparer la valeur calculée de t à celle de la distribution t (Tableau 12.A1) pour (na + nb – 2) degrés de liberté (υ). Si cette valeur de t calculée dépasse celle du niveau 5 % (colonne t = 0,05), on peut alors conclure que la vitesse moyenne a changé, à un niveau de confiance de 95 %.
Exemple
Supposons que pour une étude ponctuelle de la vitesse, les résultats obtenus sont :

Selon l’équation [EQ. 12.1] :

Comme la valeur calculée de t (9,69) est largement supérieure à 1,96 (grand nombre de degrés de liberté), il peut être conclu que la différence de vitesses moyennes (réduction de 4 km/h) est significative au niveau de confiance de 5 %.
Ce calcul peut s’effectuer à l’aide de l’utilitaire de calcul TEST DE DISTRIBUTION T
TABLEAU 12.A1 : TEST DE DISTRIBUTION T

TEST DE KOLMOGOROV-SMIRNOV
Le test « bilatéral » Kolmogorov-Smirnov permet de déterminer si deux échantillons indépendants sont tirés d’une même population (ou de populations ayant une même distribution). Dans certains cas, deux ensembles de données auront une même moyenne mais une dispersion différente, ce qui peut entraîner des problèmes de sécurité. Si les deux échantillons ont effectivement été tirés d’une même population (hypothèse nulle), on peut alors s’attendre à ce que les distributions cumulatives des deux échantillons soient rapprochées l’une de l’autre et ne devraient donc montrer qu’un écart aléatoire par rapport aux distributions de population. Si au contraire les deux distributions cumulatives d’échantillons s’éloignent trop l’une de l’autre en un point quelconque, on peut supposer qu’elles ont été tirées de populations différentes. Un écart assez important entre ces deux distributions d’échantillons justifie donc le rejet de l’hypothèse nulle.
Soit SNa(x) la fonction échelon cumulative observée pour le premier échantillon de vitesse : alors SNa(x) = K/Na où K représente le nombre de véhicules égal ou inférieur à x km/h et Na le nombre total de véhicule dans l’échantillon. Soit également SNb(x) la fonction échelon cumulative du second échantillon. Le test bilatéral de Kolmogorov-Smirnov s’intéresse à l’écart maximal D.
Pour des échantillons importants (N > 40), les tableaux de Kolmogorov-Smirnov montrent que la valeur de D doit égaler ou dépasser la valeur suivante pour rejeter l’hypothèse nulle à un niveau de 5 %, (c’est-à-dire qu’ils ne sont pas de la même population) :

Le test « unilatéral » détermine si les deux échantillons proviennent d’une même population ou si les valeurs d’un échantillon sont stochastiquement supérieures à celles de la population d’où l’autre échantillon a été tiré. Ici encore, on calcule l’écart maximal à l’aide de l’équation [EQ. 12.2] et la signification statistique de la valeur de D est déterminée en se référant à la distribution de khi-deux.
Pour des échantillons importants, la statistique suivante a une distribution d’échantillonnage qui est approximativement égale à une distribution de khi-deux à deux degrés de liberté. Voir tableau de khi-deux au Tableau 12.A2.
UTILITAIRE DE CALCUL : TEST DE KOLMOGOROV-SMIRNOV
TABLEAU 12.A2 : TABLEAU DU X2

TEST k
Le test k permet de déterminer comment les accidents ont changé à un site donné en prenant en considération les données d’accidents à un groupe de sites contrôle.
Pour un site quelconque ou un groupe de sites ayant subi un même traitement :
où:
a = accidents au site « avant » ;
b = accidents au site « après » ;
c = accidents aux sites de contrôle « avant » ;
d = accidents aux sites de contrôle « après ».
Si k < 1, il y a eu une diminution des accidents relativement aux données de contrôle ;
si k = 1, il n’y a eu aucun changement relativement aux données de contrôle ;
si k > 1, il y a eu une augmentation relativement aux données de contrôle.
Si l’une des fréquences est égale à zéro, il faut alors ajouter ½ à chaque fréquence. Dans ce cas :

L’équation suivante permet de calculer le pourcentage de changement au site :
Exemple Le Tableau 12.A3 montre les fréquences d’accidents corporels à un site en milieu semi urbain qui était à l’origine une intersection en T avec arrêt et qui a été transformée en carrefour giratoire il y a trois ans. Les données de contrôle utilisées sont les accidents survenus à toutes les autres intersections avec arrêts du district, pour des périodes avant et après identiques de trois ans. TABLEAU 12.A3 : FRÉQUENCES D’ACCIDENTS CORPORELS AU SITE DE CONTRÔLE
La notation et les équations utilisées sont celles indiquées ci-dessus : Puisque k < 1, il y a eu diminution des accidents au site par rapport aux sites de contrôle. Le pourcentage de réduction est, dans cet exemple, de 68 % : (k-1) x 100% = 68% Le calcul peut s’effectuer à l’aide de l’utilitaire de calcul TESTS AVANT-APRES (SITE INDIVIDUEL). |
TEST DU KHI-DEUX
Ce test permet de déterminer si un changement lié aux accidents est attribuable à un traitement ou s’il est dû au hasard et aurait pu se produire même si rien n’avait été fait. Le test détermine ainsi si le changement est statistiquement significatif. Il fait appel à un tableau de contingence montrant les valeurs observées pour un ensemble de données (O) et les valeurs espérées (E) si la distribution statistique n’avait pas changé. La statistique du khi-deux s’obtient en calculant :

où :
Oij = la valeur observée dans la colonne j, ligne i du tableau ;
Eij = la valeur espérée dans la colonne j, ligne i du tableau ;
m = le nombre de colonnes ;
n = le nombre de lignes.
On recherche alors cette valeur dans un tableau du khi-deux, qui indique la probabilité que les valeurs « attendues » et « observées » proviennent d’une même population. Il faut aussi connaître le nombre de degrés de liberté, qui correspond à :
Degrés de liberté (ʋ) = (n – 1) (m – 1)
Pour une étude d’accidents avec groupe de sites de contrôle et périodes similaires avant et après le traitement, on a un tableau de contingence 2 x 2 (2 colonnes et 2 lignes, avec un degré de liberté). Pour que le test soit valide, toutes les cellules de ce tableau doivent avoir une valeur minimale de 5.
En utilisant la notation du Tableau 12.A3 on peut calculer le khi-deux au moyen de l’équation suivante :

Le résultat obtenu est alors comparé aux valeurs du tableau du Khi-deux du Tableau 12.A2 à un degré de liberté (υ = 1) ; si le résultat du calcul de l’équation est supérieur à la valeur lue dans le tableau, le changement est dit statistiquement significatif, pour le niveau de confiance considéré.
Exemple À partir des données de l’exemple précédent et de l’équation [EQ. 12.9] on obtient : 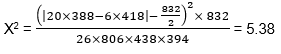 Le tableau de Khi-deux (Tableau 12.A2) indique que pour un degré de liberté (υ =1), la valeur de 5,38 se trouve entre 3,84 et 5,41. Ceci correspond à un niveau de confiance entre 0,05 et 0,02. En d’autres termes, la probabilité que le changement d’accidents observé soit attribuable à une variation aléatoire n’est que de 5 %, soit 1 chance sur 20. Cela signifie que la probabilité qu’un réel changement se soit produit dans la fréquence d’accidents à cette intersection est de 97,9 %. Un niveau de confiance de 5 % est généralement reconnu comme étant une indication sûre de l’efficacité de la mesure corrective, mais même un niveau de 10 % peut être considéré comme un indicateur de qu’un changement a déjà été produit. |
GROUPE DE SITES AYANT REÇU UN MÊME TRAITEMENT
Dans le cas d’un nombre de sites, N, ayant reçu le même traitement, le calcul de l’effet d’ensemble est plus complexe puisqu’il faut résoudre l’équation suivante pour k pour tous les sites, c’est- à-dire avec i = 1 à N. Les autres symboles sont les mêmes que dans les équations précédentes.

On utilise pour ce test le logarithme naturel de cette variable qui a une distribution plus symétrique (compatible aux traitements statistiques standards) et l’écart-type de loge k peut être approximé à l’aide de l’équation suivante :

Le ratio suivant doit alors être calculé en utilisant le logarithme loge de la valeur de k calculée ci-dessus et de son erreur-type provenant de l'expression précédente :

Si cette valeur s’écarte des valeurs limites ±1,96 (test de Student), alors le changement est considéré statistiquement significatif (à un niveau de confiance de 95 %).
Pour déterminer ensuite si les changements aux sites traités produisent effectivement le même effet sur les fréquences d’accidents, il faut calculer la valeur khi-deux suivante :

Si cette valeur est significative, avec N-1 degrés de liberté (d’après la (N-1)ème ligne du tableau du khi-deux, où N représente le nombre de sites traités), c’est que les changements aux sites ne produisent pas le même effet. Si au contraire elle n’est pas significative, alors il est probable que les changements produisent effectivement le même effet.
UTILITAIRE DE CALCUL : TESTS AVANT-APRÈS (GROUPE DE SITES)
CORRECTION DE L’EFFET DE RÉGRESSION VERS LA MOYENNE
Pour corriger l’effet de la régression vers la moyenne, il faut estimer le niveau de sécurité (la fréquence moyenne d’accidents à long terme). Plusieurs statisticiens ont proposé des méthodes pour ce faire. Ainsi, Hauer (1992) suggère de faire appel aux méthodes empiriques bayésiennes pour estimer le niveau de sécurité, et d’utiliser ensuite cette valeur (plutôt que des données brutes). Abbess et al. (1981) avaient au préalable décrit une méthode plus simple pour des sites individuels qui peut être utilisée pour corriger le biais en se basant sur certaines hypothèses de distribution statistique des accidents sur une période de plusieurs années.
Il faut recueillir les données d’accidents à des sites qui sont semblables au site traité pour des périodes identiques. À partir de cet ensemble de données est donc possible de calculer la fréquence moyenne d’accidents, a, et la variance d’accidents, var (a). L’équation suivante permet de calculer l’effet de la régression vers la moyenne R (en %) :

où :
A = nombre d’accidents au site ;
n = nombre d’années.

At et nt sont les estimés des paramètres de la distribution statistique représentant les fréquences réelles des accidents, c’est-à-dire la distribution probable de la fréquence d’accidents avant l’obtention des données. L'hypothèse principale est donc que le site étudié, avec une histoire particulière d'accidents, se comportera de la même manière que l'ensemble des sites similaires ayant la même histoire d'accidents.
Exemple Soit une intersection où il s’est produit en moyenne 15 accidents par année sur une période de 5 ans. L’intersection a été élargie, une nouvelle signalisation avec arrêts et des îlots séparateurs ont été implantés et après ces travaux, il s’y est produit en moyenne 10 accidents par année sur une période de temps similaire. Pour corriger l'effet de régression vers la moyenne, il faut sélectionner des sites d'intersections non contrôlées similaires avec des flux de trafic similaires. Si tous ces sites ont produit une moyenne, a, de 12,6 accidents par an avec une variance, var(a), de 2,91, les valeurs sont : a = 12.6 accidents/an var(a) = 2.91 (accidents/an)2 A = 75 accidents/5 ans n = 5 ans At = 12.62 / (2.91 – 12.6) = –16.38 nt = 12.6 / (2.91 – 12.6) = –1.3 L’effet de la régression vers la moyenne est donc : En d’autres termes, on aurait pu s’attendre à une diminution de 5,6 % des accidents au site durant la période « après » même si aucune intervention n’y avait été effectuée, soit une fréquence de 14,16 accidents par an. C’est ce nombre de 14,16 accidents par an qu’il faut comparer aux 10 accidents par an qui se sont effectivement produits pour déterminer si la réduction de la fréquence d’accidents attribuable aux améliorations est statistiquement significative ou non. |






