ANNEXE 10.1 - ASPECTS MÉTHODOLOGIQUES
POPULATION DE RÉFÉRENCE ET POTENTIEL D'AMÉLIORATION
Plusieurs caractéristiques des routes ont une influence sur le risque d'accident. Les routes rurales principales, qui sont conçues et exploitées selon des normes plus strictes que les routes rurales secondaires, sont généralement plus sûres en termes d'accidents par véhicule-km.
Sur une route donnée, le niveau de sécurité n'est pas constant. Par exemple, les densités d'accidents sont généralement plus faibles sur les liaisons qu'aux nœuds, en raison des différences dans le nombre de conflits de circulation. Aux nœuds, les intersections en T sont généralement plus sûres que les intersections en + pour la même raison, et ainsi de suite.
Par conséquent, le potentiel d'amélioration dépend dans une large mesure de la nature du site étudié et des modifications qui peuvent être envisagées.
Il convient donc de définir des populations de référence distinctes pour aider à déterminer ce qui constitue un niveau de sécurité représentatif pour un type de site déterminé. Ces populations sont définies en tenant compte des principales caractéristiques routières ayant un impact sur la sécurité. Par exemple, une population de référence peut être définie pour les intersections en + à deux voies en milieu urbain avec des arrêts sur les branches secondaires, une autre population pour les intersections en T sur des routes similaires, et ainsi de suite. Compte tenu de l'importance des flux de trafic dans les accidents, des populations de référence différentes devraient idéalement être développées pour différentes combinaisons de flux de trafic.
L'établissement de populations de référence requiert une bonne connaissance des facteurs contribuant à l'accident et des données disponibles qui limitent rapidement le nombre de populations possibles qui peuvent être définies. Dans la pratique, le développement de modèles statistiques multivariés est souvent utilisé pour contourner les limitations des données.
CARACTÈRE ALÉATOIRE DES ACCIDENTS
L'un des principaux problèmes posés par l'utilisation des données d'accidents pour détecter les lacunes de sécurité est lié à la nature aléatoire de ces événements.
Pour faciliter la compréhension de ce concept et de ses conséquences, utilisons un dé comme analogie. Un lancer de dé est également un événement aléatoire, dont le résultat dépend du nombre de faces du dé et de la valeur de chacune. Sur un dé standard à six faces, l'éventail des valeurs possibles est simple : [1, 2, 3, 4, 5, 6]. Lorsqu'un dé est lancé plusieurs fois, chaque face doit sortir un nombre équivalent de fois et la valeur moyenne résultante de ces lancers est 3,5 : (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3,5. Cette valeur peut être décrite comme la « moyenne à long terme » du dé. Lorsque le dé n'est lancé qu'un nombre limité de fois, par exemple trois fois, la moyenne obtenue peut varier entre les valeurs extrêmes de 1 et 6. Si ce résultat est utilisé pour estimer la moyenne à long terme du dé, la précision variera considérablement. Des variations similaires se produisent également avec les fréquences d'accidents. Le nombre d'accidents survenus sur un site au cours d'une période d'un an (f) peut être comparé à un lancer de dé, tandis que sa fréquence moyenne d'accidents à long terme (m) peut être comparée à la moyenne à long terme du dé. D'un point de vue statistique, le lancer du dé suit une distribution uniforme, tandis que les accidents suivent une distribution de Poisson.
Distribution de Poisson
où :
p(f;m) = probabilité d'observer f accidents étant donné que le niveau de sécurité est m ;
f = fréquence d’accidents ;
m = niveau de sécurité.
Il s'agit d'une équation fondamentale dans l'analyse de la sécurité routière. Elle peut être utilisée pour calculer la probabilité d'une fréquence d'accidents donnée (f) lorsque le niveau de sécurité (m) est connu. Par exemple, si la valeur m d'un site est de 5 accidents/an, la probabilité d'avoir exactement 1 accident/an est de 3,4 %, tandis que la probabilité d'avoir 6 accidents ou plus est de 38 % (Figure 10.A1). L’utilitaire de calcul « test de Poisson » peut être utilisé pour calculer cette dernière probabilité.
UTILITAIRE DE CALCUL : TEST DE POISSON

Chaque site d'un réseau routier a sa propre valeur « m » en fonction de son ensemble de caractéristiques (si l'on poursuit l'analogie avec les dés, il y aurait plusieurs dés, chacun ayant un nombre distinct de faces et de valeurs).
Dans la pratique, les difficultés proviennent du fait que le niveau de sécurité (m) est inconnu et qu'il doit être estimé (m') à partir des fréquences d'accidents rapportées (f).
Un utilitaire de calcul (UTILITAIRE DE CALCUL - INTERVALLE DE CONFIANCE) est fourni pour estimer l'incertitude de « m » sur la base d'une fréquence d'accidents observée.
Cette estimation de m devient statistiquement plus fiable à mesure que la période augmente, mais elle peut être moins représentative des conditions existantes si des changements sont intervenus sur le site au cours de la période considérée. Pour éviter ce type de biais, des périodes d'accident relativement courtes sont souvent utilisées (3 à 5 ans).
RÉGRESSION VERS LA MOYENNE
Le phénomène de régression vers la moyenne est commun à un certain nombre d'événements aléatoires et consiste en une tendance générale des valeurs extrêmes à revenir vers les valeurs moyennes. Sir Francis Galton, qui a remarqué que les enfants de parents grands étaient généralement plus petits, et vice versa, a été le premier à identifier la régression vers la moyenne au 19ème siècle (Galton, 1886). Ce phénomène s'applique également aux accidents. Lorsque la fréquence d’accidents est anormalement élevée pendant une certaine période, elle tend à diminuer pendant la période suivante et à se rapprocher de la moyenne du site à long terme (et vice versa).
BIAIS DE SÉLECTION
Le caractère aléatoire des accidents et la difficulté d'étendre les périodes d'accident autant qu'il serait nécessaire pour atteindre une précision suffisante, créent deux types de biais pendant la phase d'identification, c'est-à-dire que des sites normaux peuvent être détectés comme dangereux et que des sites dangereux peuvent ne pas être détectés. La Figure 10.A2 ci-dessous, extraite de Hauer et Persaud (1984), illustre le problème. Le rectangle représente tous les sites d'un réseau routier. L'ellipse 1 représente tous les sites dangereux (ceux dont la valeur « m » est élevée). C'est uniquement à ces endroits qu'un traitement est justifié. L'ellipse 2 représente les sites qui ont été détectés comme déviants lors de la phase d'identification (ceux dont la valeur « f » est élevée). Quatre types de situations peuvent se présenter (domaines A à D) :
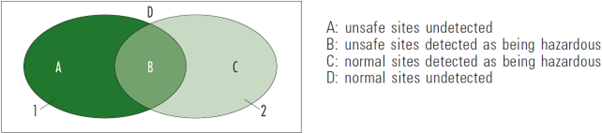
L'objectif de l'étape d'identification est d'obtenir la meilleure superposition possible des ellipses 1 et 2 et de limiter les zones A et C. Les techniques d'identification qui prennent en compte le caractère aléatoire des accidents sont considérées comme réduisant le biais de sélection.






