ANNEXE 10.2 – PROCÉDURES ET EXEMPLES

FRÉQUENCE D’ACCIDENTS

Procédure

Exemple (voir Tableaux 10.A2 et 10.A3)

  1. Localiser tous les accidents rapportés au cours de la période d'analyse

 

  1. Définir les différentes populations de référence

 

  1. Pour chaque population de référence :
  • Calculer la fréquence d'accidents sur chaque site 
  • Calculer la fréquence moyenne d’accidents dans la population de référence :
  1. où :
  2. frp = fréquence moyenne d’accidents
  3. fj = fréquence d’accidents sur le site j d’une population de référence 
  4. n = nombre de sites
  • Déterminer la fréquence minimum d'accidents qui justifie une analyse détaillée de la sécurité (IT)

Routes rurales à deux voies

La fréquence d'accidents est comprise entre 0 et 14 accidents (colonne 3 du Tableau A10.2.2).

 

 

 

frp  = 258 accidents / 55 sites 
= 4,69 accidents / site

 

 

 

 

 

IT = 2 x frp = 9,38 (9 accidents)

Sections 1,10,12,45 et 52 sont détectées

TAUX D’ACCIDENTS

Procédure

Exemple (voir Tableaux 10.A2 et 10.A3)

  1. Localiser tous les accidents rapportés au cours de la période d'analyse

 

  1. Définir les différentes populations de référence

 

  1. Pour chaque population de référence :
  • Calculer le taux d'accidents de chaque site
  1. où :
  2. Rj = taux d'accidents du site j (accidents/Mveh-km)
  3. Rrp = taux moyen d'accidents (accidents/Mveh-km)
  4. fj = fréquence d'accidents sur le site j
  5. P = période d'analyse (années)
  6. Lj = longueur de la section du site j (km)
  7. Qj = trafic moyen journalier annuel du site j (TMJA) 
  • Calculer le taux moyen d’accidents pour la population de référence :

où :

Rrp = taux moyen d’accidents (accident/Mveh-km)

fj = fréquence d'accidents sur le site j

P = période d'analyse (années)

Lj = longueur de la section du site j (km)

Qw = trafic moyen journalier annuel pondéré (TMJA)

Qj = TMJA du site j

  • Déterminer le taux d'accidents minimum justifiant une analyse détaillée de la sécurité (IT)

Routes rurales à deux voies

Pour la section #1 :

 

 

= 2,72 accidents/ Mveh-km

Le taux d'accidents est compris entre 0 et 4,73 accidents/Mveh-km (colonne 4 du Tableau A10.2.2)

 

 

 

 

 

 

 

 

 

= 1,94 accidents/Mveh-km

 

 

 

 

 

 

 

 

 

 

 

IT   = 2 x Rrp  
= 2 x 1,94 = 3,88 accidents/Mveh-km

Sections 10, 33, 35 et 39 sont détectées

Note : pour les intersections, L n’est pas considéré, et les taux critiques d’accidents sont exprimés en termes d’accidents/Mveh.

UTILITAIRE DE CALCUL : TAUX D’ACCIDENTS 

TAUX D’ACCIDENTS CRITIQUE

Procédure

Exemple (voir Tableaux 10.A2 et 10.A3)

  1. Localiser tous les accidents rapportés au cours de la période d'analyse

 

  1. Définir les différentes populations de référence

 

  1. Pour chaque population de référence :
  • Calculer le taux d'accidents sur chaque site [EQ. 10.8]
  • Calculer le taux moyen d'accidents pour la population de référence [EQ. 10.9]

Routes rurales à deux voies

Colonne 4 in Tableau A10.2.2

Pour la section #1 : 

R1   = 2,72 accidents/Mveh-km

Rrp  = 1,94 accidents/Mveh-km

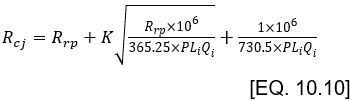  • Calculer le taux critique de chaque site :

où :

Rcj = taux d'accidents critique sur le site j 

(accidents/Mveh-km)

Rrp = taux moyen d'accidents sur des sites similaires (accidents/ Mveh-km)

K = constante statistique :

1,036 pour un niveau de confiance de 85%

1,282 pour un niveau de confiance de 90%

1,645 pour un niveau de confiance de 95%

2,326 pour un niveau de confiance de 99%

P = période d'analyse (années)

Lj = longueur de la section j (km)

Qj = trafic moyen journalier annuel sur le site j (TMJA)

Pour la section #1, avec un niveau de confiance de 85% :

 

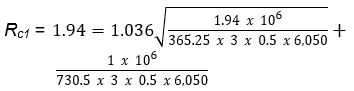          = 2,89 accidents/Mveh-km

(Colonne 5 du Tableau A10.2.2)

Les taux critiques d'accidents varient de 2,72 à 5,27 accidents/Mveh-km

  • Comparer le taux d'accidents et le taux d'accidents critique sur chaque site. Une analyse de sécurité détaillée est justifiée lorsque le taux d'accidents est supérieur au taux critique

Les sections 10, 35 et 45 sont détectées (niveau de confiance de 85%)

Note : pour les intersections, L n'est pas considéré, et les taux d'accidents critique sont exprimés en termes d'accidents/Mveh

UTILITAIRE DE CALCUL : TAUX D’ACCIDENTS CRITIQUE 

INDICE ÉQUIVALENT DE DOMMAGES MATÉRIELS SEULEMENT (IEDMS)

Procédure

Exemple (voir Tableaux 10.A2 et 10.A3)

  1. Localiser tous les accidents rapportés au cours de la période d'analyse

 

  1. Définir les différentes populations de référence

 

  1. Sélectionner les facteurs de pondération pour chaque catégorie de traumatismes

Les facteurs de pondération proposés par Agent (1973) sont utilisés dans cet exemple :

1,0 pour les accidents avec dommages matériels seulement (DMS)
3,5 pour les accidents avec blessures sans gravité
9,5 pour les accidents mortels ou avec blessures graves 

  1. Pour chaque population de référence :
  • Calculer l’IEDMS et l’IEDMS moyen () de chaque site:

 où :

IEDMSj = indice équivalent de dommages matériels seulement sur le site j

wi = facteur de pondération pour un accident de gravité i

fij = fréquence d'accidents de gravité i sur le site j

Où :

= IEDMS moyen au site j

fj = fréquence totale d'accidents sur le site j

  • Calculer le moyen dans la population de référence (IEDMSrp) :
  • Déterminer la valeur minimum de l'IEDMS justifiant une analyse détaillée de la sécurité (IT)

Routes rurales à deux voies

Pour la section #1 :

 

 

 

IEDMS1 = 2 x 9,5 + 3 x 3,5 + 4 x 1 = 33,5

Colonne 6 du Tableau A10.2.2

IEDMS intervalle de 0 à 33,5

 

 

 

 

1= 33,5 / 9 = 3,72

Colonne 7 du Tableau A10.2.2

intervalle de 0 à 4,67

 

 

 

 

 

 

= 2,16

IT = 2 x rp

IT = 2 x 2,16 = 4,32

Les sections 33 et 49 sont détectées

UTILITAIRE DE CALCUL : IEDMS 

INDICE DE GRAVITÉ RELATIVE (IGR)

Procédure

Exemple (voir Tableaux 10.A2 et 10.A3)

  1. Localiser tous les accidents rapportés au cours de la période d'analyse

 

  1. Définir les différentes populations de référence

 

  1. Pour chaque population de référence :
  • Calculer le coût moyen de chaque type d’accident dans la population de référence :
  • Calculer le IGR et le moyen de chaque site

où :

IGRj = indice de gravité relative dans le site j

fij = fréquence d'un accident de type i sur le site j

Ci= coût moyen d'un accident de type i

Où :

fj = fréquence totale d'accidents sur le site j

  • Calculer le IGR () moyen de la population 
  • Déterminer la valeur minimum de IGR justifiant une analyse détaillée de la sécurité (IT)

Routes rurales à deux voies

Une grille de coûts doit être élaborée en se basant sur des données nationales. Les valeurs du Tableau 10.3 sont utilisées dans cet exemple.

Pour la section #1 :

IGR1 =  (2 x 104 600 $) + (2 x 173 200 $) + (1 x 175 900 $) + (2 x 109 700 $) + (2 x 341 600 $) = 1 634 100 $

=  1 634 100 $ / 9 = 181 567 $

 

Colonnes 8 et 9 du Tableau A10.2.2

IGR intervalle de 0 $ to 2 707 500 $

intervalle de 0 $ to 237 200 $

 

 

 

 

 

 

 

 

 

= 162 817 $

IT = 2 x = 2 x 162 817 $ = 325 634 $

Aucune section n'est détectée par ce critère

CRITÈRES COMBINÉS (FRÉQUENCE ET TAUX)

Procédure

Exemple (voir Tableaux 10.A2 et 10.A3)

  1. Localiser tous les accidents rapportés au cours de la période d’analyse

 

  1. Définir les différentes populations de référence

 

  1. Pour chaque population de référence :
  • Calculer la fréquence et le taux d'accidents sur chaque site [EQ. 10.8]

Routes rurales à deux voies

Colonnes 3 et 4 du Tableau A10.2.2

  • Calculer la fréquence moyenne d'accidents et le taux moyen d'accidents dans la population de référence [EQ. 10.7] et [EQ. 10.9]

frp      = 4,69 accidents par site

Rrp   = 1,94 accidents/Mveh-km

  • Déterminer la fréquence et le taux d'accidents minimums justifiant une analyse détaillée de la sécurité

Seuils minimaux d'investigation :

2 x frp and 2 x Rrp

  • Classer les sites selon les critères de détection suivants

IT = 2 x frp = 2 x 4,69 = 9,38 accidents

IT = 2 x Rrp = 2 x 1,94 = 3,88 accidents/Mveh-km

Selon cette combinaison de critères, la section 10 justifie une analyse détaillée

PROPORTION BINOMIALE

Procédure

Exemple

  1. Localiser tous les accidents rapportés au cours de la période d’analyse

 

  1. Définir les différentes populations de référence

 

  1. Pour chaque population de référence :
  • Calculer la fréquence totale d'accidents et la fréquence de chaque type d'accident considéré, sur chaque site.
  • Calculer la proportion de chaque type d'accident considéré dans la population de référence

Routes rurales à deux voies

État de la surface (population de référence et section #45) : Sur les 12 accidents rapportés sur la section #45, 7 sont survenus sur des surfaces mouillées (58 %). La proportion équivalente dans la population de référence est de 27 %

  • Calculer P(Fij ³ fij) basée sur [EQ. 10.4]

Pour les surfaces mouillées : Les probabilités d'observer 0, 1, ...6 accidents sur surface mouillée à la section #45 et les probabilités cumulatives correspondantes sont les suivantes.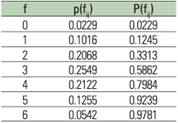

La probabilité d'observer 6 accidents ou moins sur surface mouillée est de 98%. Par conséquent, la probabilité d'en observer 7 ou plus n'est que de 2 % (c'est-à-dire que la fréquence des accidents sur chaussée mouillée est anormalement élevée à ce site)

UTILITAIRE DE CALCUL : TEST BINOMIALE

MODÈLE DE PRÉDICTION D’ACCIDENTS

Procédure

Exemple (voir Tableaux 10.A2 et 10.A3)

  1. Localiser tous les accidents rapportés au cours de la période d’analyse

 

  1. Définir les différentes populations de référence

 

  1. Pour chaque population de référence :
  • Déterminer la fréquence d'accidents et le volume de trafic sur chaque site
  • Développer le modèle de prédiction d'accidents pour la population de référence

Routes rurales à deux voies

Colonnes 2 et 3 du Tableau A10.2.2

Le modèle suivant a été appliqué aux 55 sections de cet exemple :

fp = 0,0084 Q0,76

où :

fp = fréquence d'accidents prévue / 3 ans

Q = trafic moyen journalier annuel (TMJA)

  • Calculer la fréquence d'accidents estimée à chaque site à l'aide du modèle de prédiction d'accidents (fpj)

Pour la section 1 :

fp1 = 0,0084 × 60500,76 = 6,07 accidents/3 ans

Colonne 10 du Tableau A10.2.2

fp intervalle de 1,31 à 7,84 accidents/3 ans 

  • Calculer le potentiel d'amélioration (P.A.) de chaque site

P.A.j = fj - fpj

Pour la section 1 :

P.A.1 = 9-6,07 = 2,93 accidents/3 ans 

Colonne 11 du Tableau A10.2.2

P.A. intervalle de 4,56 to 8,43 accident/3 ans

  • Classer les sites en fonction de leur potentiel d'amélioration

Les sections 10, 45, 1, 36 et 52 présentent le potentiel d'amélioration le plus élevé

Le tableau suivant présente un résumé des résultats obtenus avec l'exemple numérique.

Cela montre que :

  • La section 10 a été détectée par 6 de ces 8 critères d'identification. Il est clair que cette section présente un problème de sécurité. Lorsque le problème est évident, le choix des critères d'identification a moins d'impact sur la sélection des sites ;
  • Le critère de fréquence d'accidents a permis de détecter principalement les sections présentant des volumes de trafic élevés (à l'exception de la section 10, chaque section détectée présente un volume de trafic journalier supérieur à 6 000 véhicules, alors que le TMJA moyen est de 4 400 véhicules). En revanche, le critère du taux d'accidents a permis de détecter principalement des sections à faible volume de trafic (à l'exception de la section 10, toutes les sections détectées ont un volume de trafic journalier inférieur à 2 000 véhicules). Il s'agit d'un résultat typique pour ces critères ;
  • Trois critères utilisent directement le concept de potentiel d'amélioration pour classer les sections ou ses variantes : la fréquence d'accidents, le modèle de prédiction d'accidents et les méthodes empiriques bayésiennes (EB). Cependant, il existe des différences dans les sections identifiées. Les résultats obtenus avec le modèle de prédiction d'accident sont considérés comme plus fiables que ceux obtenus avec le critère de fréquence d'accidents car l'estimation de la fréquence d'accidents moyenne (population de référence) est plus précise. De même, les résultats obtenus à l'aide des méthodes EB sont jugés plus fiables que ceux obtenus à l'aide du modèle de prédiction, car ils améliorent également la précision de la fréquence d'accidents sur un site.

Bien qu'il ne soit pas possible de tirer des conclusions définitives à partir d'un exemple, celui-ci illustre néanmoins comment la détection des sites peut différer en fonction du critère de détection utilisé. C'est pourquoi il est fortement recommandé d'utiliser plusieurs critères d'identification et de comparer les résultats obtenus.

TABLEAU 10.A2 : EXEMPLE – DONNÉES SUR LES ACCIDENTS (01/01/98 À 31/12/00)

TABLEAU 10.A3 : EXEMPLE – RÉSULTATS